Méthodes d'intégration

Au début de la section précédente, nous avons présenté une équation permettant de calculer la trajectoire d'un projectile. Cette équation est obtenue par la résolution d'une intégrale. Or, en pratique, il est très rare que l'utilisation d'une intégration symbolique soit possible en raison de l'aspet dynamique de l'environnement simulé. Par exemple, il faut tenir compte des collisions, des changement d'accélération, des commandes de l'usager, etc. Pour ces raisons, nous avons recours à l'intégration numérique, ce qui consiste à calculer itérativement des équations plusieurs fois par seconde.

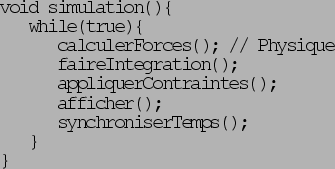
Ordinairement, la méthode d'intégration est appelée dans une boucle de simulation telle que montrée à la figure 3. En premier lieu, on calcule les forces appliquées sur les objets, comme la gravité, la friction avec l'air (vent), les tensions exercées par les ressorts, etc. Ensuite, à l'aide des forces calculées, on fait une intégration. Après, si nécessaire, on peut appliquer des contraintes, comme la détection de collision. En dernier lieu, on peut procéder à l'affichage et synchroniser le temps de simulation avec le temps réel.

Figure 3: Précédure générale de simulation